Booleova algebra. Dio 2. Osnovni zakoni i funkcije

Nastavak priče o Booleovoj algebri, konvencijama, pravilima, operacijama. Prijelaz na osnove kontaktnih sklopova.

prvi članak George Bull opisan je kao tvorac algebre logike. U drugom članku opisane su osnovne operacije boolove algebre i metode za pojednostavljivanje logičkih izraza. Dakle, Booleova algebra koristi izjave kao argumente, i ne njihovo značenje, već istinu ili neistinitost izjave.

Obrazac za pisanje izraza u Booleovoj algebri.

Ako je izjava istinita, onda se piše ovako: A = 1, ako je lažna, onda je A = 0 (uostalom, nije istina da je krumpir voće). Za bilo koju tvrdnju, A je ili istinita (A = 1) ili lažna (A = 0). Ovdje ne može biti sredina. O tome smo već razgovarali.

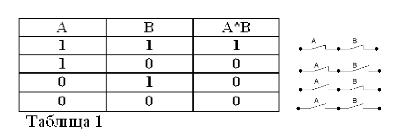
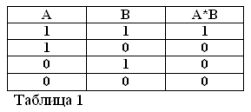
Ako spojite dvije jednostavne izjave sa unijom I, dobit ćete složenu izjavu koja se zove logički proizvod. Uzmimo dvije jednostavne izreke: „Tri je više od dva“ mi ćemo označiti slovom A, „Tri manje od pet“ - slovom B.

Stoga je složena izjava "Tri je više od dvije A manje od pet" logična (u ovom slučaju velika slova A, kaže da je ovo logička operacija "I", kao i kasnije u tekstu "ILI" i "NE"). i B. Označava se kako slijedi: A ^ B ili A * B.

Logičko množenje (operacija "I").

U elementarnoj algebri A * A = A2. Ali u Buhovoj algebri A * A = A2 = A, A * A = A, jer znak množenja (*) sada znači ... I ... u smislu And ... I. Sve naše iskustvo potvrđuje da je A&A isto što i A. Samo se ne mogu složiti s tim. Istina izjave ne mijenja se ako je faktor ponovljen nekoliko puta.

Proizvod dviju izjava smatra se istinitim (jednakim 1), tada i samo ako su oba čimbenika istinita, i lažnim (jednakim 0) ako je barem jedan od faktora lažan. Slažete se da se ta pravila ne suprotstavljaju zdravom razumu i, osim toga, u potpunosti su u skladu s pravilima elementarne algebre:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Prva jednakost glasi kako slijedi: ako su i A i B istinite, tada je proizvod A * B istinit. U Buhlovoj algebri znak množenja (*) zamjenjuje sjedinjenje I.

Logični proizvodi mogu uključivati ​​ne dva, već veći broj izjava - faktora. U ovom je slučaju proizvod istinit samo ako su istodobno istiniti svi iskazi-faktori.

Logički dodatak (ILI rad)

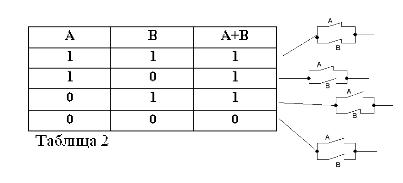
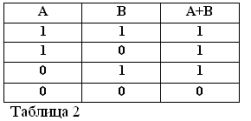
Ako su dvije izjave povezane sindikatom ILI. ta formirana složena rečenica naziva se logičkim zbrojem.

Razmotrimo primjer logičnog zbroja. Reći A: "Danas ću ići u kino."

Izjava B: „Danas ću ići u disko.“ Dodamo obje izjave i dobijemo: "Danas ću ići u kino ili u disko."

Ova složena izjava označava se kako slijedi: A + B = C ili (A V B) = C.

Pomoću C označili smo složenu izjavu logičkog zbroja.

U primjeru koji se razmatra, sindikat ILI ne može se koristiti u isključivom smislu. Doista, istog dana možete doći u kino i disko. A evo izreke:

"Predsjednik vrtlarskog partnerstva bit će Petrov ili Ivanov", nije logičan zbroj, jer samo će jedna osoba biti predsjednik, a druga amaterski obični vrtlar.

Znak V za logički zbroj je odabran jer je početno slovo latinske riječi "vel", što znači "ili", za razliku od latinske riječi "aut>, što znači" i ". Sada bi svima trebalo biti jasno zašto je logički proizvod označen znakom ^.

U elementarnoj algebri postoji pravilo A + A = 2A. Ovo je pravilo tačno, bez obzira na to koji je broj predstavljen slovom A. U bulovoj algebri njemu odgovara pravilo A + A = A. Cijelo naše životno iskustvo kaže da reći A ILI A ili oba A samo je još jedan i duži način da kažeš samo A.

Kao i svaka složena izjava, zbroj dviju izjava A i B može biti istinit ili lažan. Zbroj se smatra istinitim, odnosno jednak je jedinstvu, ako je barem jedan od uvjeta istinit:

A + B = 1 ako je OR A = 1 ILI B = 1, što je u skladu s uobičajenom aritmetikom:

1+0 = 0+1 = 1.

Ako su obje zbrojene izjave istinite, tada se i zbroj smatra istinitim, dakle, u буovoj algebri imamo: (1) + (1) = 1.

Uglati zagrade su ovdje postavljeni kako bi se naglasilo uvjetno, značenje ovog dodatka, a ne aritmetika.

Zbroj dviju izjava smatra se lažnim i jednak je nuli ako, ali samo ako su oba izraza lažna. Odavde:

0 + 0=0.

Dakle, zbroj dviju izjava A + B smatra se istinitim ako je istina, ILI A, ILI B, ILI oba pojma zajedno. Dakle, riječ ILI označena je sa +.

Sjećajući se da izjave A i B mogu biti samo istinite ili lažne i, prema tome, imaju mjeru istine 1 ili 0, rezultati razmatranih operacija AND i OR mogu se sažeti u tablice 1 i 2.

Treća operacija koju široko koristi Buhlova algebra je negacija - NE. Podsjećamo da osnovna algebra koristi operacije ADD, D Oduzimanje, Pomnoži s, Podijeli i neke druge.

Za svaku tvrdnju A postoji negacija NE A, koju ćemo označiti simbolom / A. Ovo ne bi trebalo biti u dvojbi.

Dajemo primjere: „Ići ćemo u šumu“ A, „Nećemo u šumu“ / A.

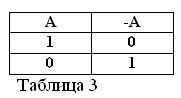
Ako je izjava A istinita, odnosno A = 1, onda njena negacija / A mora biti lažna / A = 0. I obrnuto, ako je neka tvrdnja lažna, onda je njena negacija tačna. Na primjer: „Konj ne jede sijeno“ / A = 0, „Konj ne jede sijeno“ (A = 1). To se može izraziti u tablici 3.

Utvrđujući značenje akcije negacije i pretpostavljajući da je od dvije izjave A i / A uvijek jedna istina, slijede dvije nove formule booleove algebre:

A + (/ A) = 1 i A * (/ A) = 0.

Postoje i druge formule koje pojednostavljuju logičku obradu izjava. Na primjer, 1 + A = 1, jer, prema definiciji zbrajanja, u slučaju kada je jedan izraz jednak jedinici, zbroj je uvijek jednak. Dobiveni rezultat ne ovisi o tome je li A = 0 ili A = 1.

Svaka od tri logičke operacije koje smo ispitivali (I, ILI, NE) ima određena svojstva koja su bliska pravilima elementarne algebre. Ako su svi formulirani, tada dobivamo 25 pravila boolove algebre. Sasvim su dovoljni da riješe gotovo svaki logički problem. Bez ovih pravila postaje prilično teško riješiti logičke probleme zbog njihove prividne složenosti. Pokušati pronaći točan odgovor bez korištenja pravila znači zamijeniti ih domišljatošću i općim razumom. Pravila uvelike olakšavaju ovaj rad i štede vrijeme.

U okviru članka nemoguće je razmotriti svih tih 25 pravila, ali oni koji to žele uvijek ih mogu naći u odgovarajućoj literaturi.

Kao što je već spomenuto u prvom članku 1938. godine, mladi američki znanstvenik Claude Shannon, u svom članku „Simbolička analiza relejnih i prekidačkih krugova“, prvi put koristi booleovu algebru za probleme relejne tehnologije. Shannonovo otkriće bilo je da je shvatio da je metoda projektiranja relejnih strojeva i elektroničkih računala zapravo grana matematičke logike.

To se često događa. Znanstvenik dugi niz godina radi na problemu koji svojim sunarodnjacima izgleda potpuno nepotreban - samo zabavi. Ali prolaze desetljeća, a ponekad i stoljeća, a teorija koja nikome nije potrebna ne samo da stječe pravo na postojanje, već i bez toga daljnji napredak postaje nezamisliv.

Što je pomoglo Shannonu da drugi put otkrije booleovu algebru? Slučaj? Ništa takve vrste.

Ljubav prema relejnim strojevima, izgrađenim na konvencionalnim prekidačima i relejima, pomogla je mladom znanstvenici da poveže zaboravljenu teoriju sa zadacima automatskih telefonskih centrala, na kojima je radio u to vrijeme. Potom je Shannon uveo istu ideju "da ili ne" u diskretne poruke i postavio temelje čitavom dijelu kibernetike - teorije informacija.

Buhlova algebra bila je vrlo pogodna za analizu i sintezu relejnih krugova. Bilo je dovoljno prihvatiti kao istinitu tvrdnju: "U krugu postoji signal", a kao lažna - "Nema signala u krugu", jer se pojavila nova algebra - signalna algebra, algebra relejnog kruga.

Nova algebra vrijedi samo za razmatranje relejnih i sklopnih krugova. Uostalom, samo u takvim shemama je uvjet „postoji signal“ i „nema signala“. Ako se signal neprekidno mijenja, stječući proizvoljno velik broj intermedijarnih uvjeta (takav se signal naziva analogni), relejna algebra nije primjenjiva. To se uvijek mora zapamtiti. Ali samo većina elektroničkih računala i kibernetskih strojeva koristi diskretni princip obrade signala, koji se temelji na elementima „da - ne“.

Izraz "Kontakt je zatvoren" Shannon je prihvatio kao istinit (1), a "Kontakt otvoren" kao lažan (0). Ostatak "algebre", uključujući operacije AND, OR i NOT i 25 pravila, Shannon je posudio od Boolea.

Algebra relejnog kruga pokazala se jednostavnijom od Boolove algebre jer se bavi samo elementima tipa "da - ne". Uz to je nova algebra vizualnija.

Elementi u ovoj algebri su kontakti, koje ćemo označiti slovima A, B, C ... Kontakt je zatvoren - A, kontakt je otvoren - / A (slovo s crticom).

Notacija je, kao što vidite, u potpunosti preuzeta iz boolove algebre. Otvoreni kontakt negacija je zatvorenog kontakta. Isti kontakt ne može biti i zatvoren i otvoren.

Dogovorimo se da ako su u bilo kojem krugu dva kontakta označena istim slovom, to znači da uvijek uzimaju iste vrijednosti.

U bilo kojem trenutku oboje su ili istovremeno otvorene ili su oboje zatvorene. Najlakši način da ih zamislite mehanički povezani zajedno, tako da se oboje istovremeno otvaraju ili zatvaraju.

Ako je u nekom lancu kontakt negacija drugog kontakta, tada je njihovo značenje uvijek suprotno. Na primjer, kontakti C i / C nikada ne mogu biti istovremeno otvoreni ili istovremeno zatvoreni. I na dijagramu se mogu predstaviti mehanički povezani: ako se jedan od njih otvori, onda se drugi zatvara.

Svoje upoznavanje s relejskom algebrom započinjemo analizom najjednostavnijih krugova koji odgovaraju operacijama AND, OR i NOT.

Proizvod dva kontakta (operacija I) je sklop dobiven kao rezultat njihove serijske veze: on je zatvoren (jednak 1) samo kad su oba kontakta zatvorena (jednaka 1).

Zbroj dva kontakta (operacija ILI) bit će krug formiran kada su paralelno povezani: on je zatvoren (jednak 1) kada je barem jedan kontakt koji tvori krug zatvoren (jednak 1).

Suprotnost ovom kontaktu (operacija NE) je kontakt jednak 0 (otvoren) ako je kontakt 1 (zatvoren), i obrnuto.

Kao u booleovoj algebri, ako su kontakti označeni slovima A i B, tada ćemo produkt dva kontakta označiti s A * B, zbroj s A + B, a kontakt nasuprot A, sa / A. Navedeno je objašnjeno na slikama 1, 2 i 3.

Valjanost tablica koje odgovaraju operacijama AND, OR i NOT. sada nitko ne bi trebao biti u dvojbi.

Zaustavimo se na dva primjera: 1 * 0 = 0 i 1 + 0 = 1.

Iz slike se vidi da je trajno zatvoren kontakt povezan u seriju s stalno otvorenim kontaktom ekvivalent trajno otvorenom kontaktu (1 * 0 = 0) Trajno zatvoreni kontakt povezan paralelno s stalno otvorenim kontaktom ekvivalentan je trajno zatvorenom kontaktu.

Upoznavši se s aritmetikom kontaktnih krugova, možete opisati bilo koji relejni krug formulom pomoću prihvaćenih konvencija. U kibernetikama se takve formule nazivaju strukturalnim.

Ako je strukturna formula bilo kojeg relejnog kruga 1, tada signal može proći kroz njega - krug je zatvoren. Suprotno tome, ako je strukturna formula kruga 0, signal neće proći kroz nju - krug je prekinut.Zaključak: dva relejna kruga jednaka su jednakom drugom kada su njihove strukturne formule jednake.

U nastavku članka razmotrit ćemo primjere kontaktnih krugova, tipičnih kontaktnih krugova i njihovih ekvivalenata, kao i crtanje dijagrama prema strukturnim formulama. Također smatramo glavne logičke sklopove koji obavljaju funkcije Boolove algebre.

Nastavak članka: Booleova algebra. Dio 3. Sheme kontakata

Boris Aladyskin